Hyperspectral Imagery
Unsupervised and supervised band selection
Common problems in the area of hyperspectral analysis involving data relevancy include optimal selections of wavelength, number of bands, and spatial and spectral resolution. Additional issues include the modeling issues of scene, sensor and processor contributions to the measured hyperspectral values, finding appropriate classification methods, and identifying underlying mathematical models.
Part of this project is a development of a new methodology for combining unsupervised and supervised methods under classification accuracy and computational requirement constraints that is designed to perform hyperspectral band (wavelength range) selection and statistical modeling method selection. The band and method selections are utilized for prediction of continuous ground variables using airborne hyperspectral measurements.
We address the issue of hyperspectral band and method selection using unsupervised and supervised methods driven by classification accuracy and computational cost. The problem is formulated as follows: Given N unsupervised band selection methods and M supervised classification methods, how would one obtain the optimal number of bands and the best performing pair of methods that maximize classification accuracy and minimize computational requirements?
Unsupervised methods for band selection: Unsupervised methods order hyperspectral bands without any training and the methods are based on generic information evaluation approaches. Unsupervised methods are usually very fast and computationally efficient. These methods require very little or no hyperspectral image pre-processing. For instance, there is no need for image geo-referencing or registration using geographic referencing information, which might be labor-intensive operations
- Method 1: Information Entropy - This method is based on evaluating each band separately using the information entropy measure based on the the probability density function of reflectance values in a hyperspectral band and the number of distinct reflectance values. The probabilities are estimated by computing a histogram of reflectance values. Generally, if the entropy value H is high then the amount of information in the data is large. Thus, the bands are ranked in the ascending order from the band with the highest entropy value (large amount of information) to the band with the smallest entropy value (small amount of information).
- Method 2: First Spectral Derivative - The bandwidth, or wavelength range, of each band is a variable in a hyperspectral sensor design. This method explores the bandwidth variable as a function of added information. It is apparent that if two adjacent bands do not differ greatly then the underlying geo-spatial property can be characterized with only one band. Thus, if derivative is equal to zero then one of the bands is redundant. In general, the adjacent bands that differ significantly should be retained, while similar adjacent bands can be reduced.
- Method 3: Second Spectral Derivative - Similar to the first spectral derivative, this method explores the bandwidth variable in hyperspectral imagery as a function of added information. If three bands are adjacent, and the two outside bands can be used to predict the middle band through linear interpolation, then the band is redundant. The larger the deviation from a linear model, the higher the information value of the band.
- Method 4: Contrast measure - This method is based on the assumption that each band could be used for classification purposes by itself. The usefulness of a band would be measured by a classification error achieved by using only one particular band and minimizing the error. In order to minimize a classification error, it is desirable to select bands that provide the highest amplitude discrimination (image contrast) among classes. If the class boundaries were known a priori then the measure would be computed as a sum of all contrast values along the boundaries. However, the class boundaries are unknown a priori in the unsupervised case. One can evaluate contrast at all spatial locations instead assuming that each class is defined as a homogeneous region (no texture variation within a class). In general, bands characterized by a large value of ContrastM are ranked higher (good class discrimination) than the bands with a small value of Contrast.
- Method 5: Spectral Ratio Measure - In many practical cases, band ratios are effective in revealing information about inverse relationship between spectral responses to the same phenomenon (e.g., living vegetation using the normalized difference vegetation index. This method explores the band ratio quotients for ranking bands and identifies bands that differ just by a scaling factor. The larger the deviation from the average of ratios E(ratio) over the entire image, the higher the RatioM value of the band.
- Method 6: Correlation Measure - One of the standard measures of band similarity is normalized correlation. The normalized correlation metric is a statistical measure that performs well if a signal-to-noise ratio is large enough. This measure is also less sensitive to local mismatches since it is based on a global statistical match. The correlation based band ordering computes the normalized correlation measure for all adjacent pairs of bands similar to the spatial autocorrelation method applied to all ratios of pairs of image bands. After selecting the first least correlated band based on all adjacent bands, the subsequent bands are chosen as the least correlated bands with the previously selected bands.
- Method 7: Principal Component Analysis Ranking (PCAr) - Principal component analysis has been used very frequently for band selection in the past. The method transforms a multidimensional space to one of an equivalent number of dimensions where the first dimension contains the most variability in the data, the second the second most, and so on. The process of creating this space gives two sets of outputs. The first is a set of values that indicate the amount of variability each of the new dimensions in the new space represents, which are also known as eigenvalues. The second is a set of vectors of coefficients, one vector for each new dimension, that define the mapping function from the original coordinates to the coordinate value of a particular new dimension. The mapping function is the sum of the original coordinate values of a data point weighted by these coefficients. As a result, the eigenvalue indicates the amount of information in a new dimension and the coefficients indicate the influence of the original dimensions on the new dimension. Our PCA based ranking system (PCAr) makes use of these two facts by scoring the bands.
Supervised methods for band selection: Supervised methods require training data in order to build an internal predictive model. A training data set is obtained via registration of calibrated hyperspectral imagery with ground measurements. Supervised methods are usually more computationally intensive than unsupervised methods due to an arbitrarily high model complexity and an iterative nature of model formation. Another requirement of supervised methods is that the number of examples in a training set should be sufficiently larger than the number of attributes (bands, in this case). If taken alone, the unsupervised methods can, at best, be used to create classes by clustering of spectral values followed by assigning an average ground measurement for each cluster as the cluster label. Supervised methods therefore provide more accurate results than unsupervised methods.
- Method 1: Regression - The regression method is based on a multivariate regression that is used for predicting a single continuous variable given multiple continuous input variables. The model building process can be described as follows. Given a set of training examples T, find the set of coefficients that gives the minimum value of g(T) using the observed output variable of a training example. The problem can be solved numerically using well-known matrix algebra techniques.
- Method 2: Instance based (k-nearest neighbor) - The instance based method uses inverse Euclidean distance weighting of the k-nearest neighbors to predict any number of continuous variables. To predict a value of the example being evaluated, the k points in the training data set with the minimum distance to the point over the spectral dimensions are found. The weighting factor used is raised to the power w. Altering the value of w therefore influences the relationship between the impact of a training point on the final prediction and that training point’s distance to the point being evaluated. The user must set the values of the control parameters k and w.
- Method 3: Regression tree algorithms - A regression tree is a decision tree that is modified to make continuous valued predictions. They are akin to binary search trees where the attribute used in the path-determining comparison changes from node to node. The leaves then contain a distinct regression model used to make the final prediction. To evaluate (or test) an example using a regression tree, the tree is traversed, starting at the root, by first comparing the reflectance value at a single wavelength requested by the node and compared to the split-point. Particular wavelengths may be used by several nodes or none at all. If the reflectance value of the example at the appropriate wavelength is less than the split point, the left branch is taken, if greater than or equal to the split-point, the right. This splitting procedure based on reflectance values continues until a tree leaf is encountered, at which time the prediction can be made based on data in the leaf.
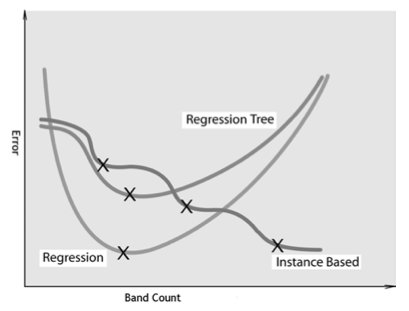
Expected trends based on the models of three supervised methods.
Expected Trends
Assuming that each unsupervised method sorts the bands based on band redundancy in ascending order, our expectation is to see the following trends in the resulting function. First, the regression-based supervised method is using a global modeling approach where very few bands (insufficient information) or too many bands (redundant information) will have a negative impact on the model accuracy. Thus, we expected the trend of a parabola with one global minimum. Second, the instance- based method exploits local information and adding more bands will either decrease an error or preserve it constant. The expected trend is a down-sloped staircase curve with several plateau intervals. The beginning of each plateau interval can be considered as a local minimum for selecting the optimal number of bands (see crosses in Figure). Lastly, the regression tree based method uses a hybrid approach from a standpoint of local versus global information. It is expected to demonstrate a trend of the instance based method for a small number of processed bands (band count) and a trend of the regression-based method for a large number of processed bands.

Results and Conclusions
In this experiment, the goal was to select a combination of unsupervised and supervised methods, the optimal number of bands, and band indices subject to model accuracy and computational requirement considerations.
The hyperspectral image data used in this work were collected from an aerial platform with a Regional Data Assembly Centers Sensor (RDACS), model hyperspectral (H-3), which is a 120-channel prism-grading, push-broom sensor developed by NASA. Each image has 2500 rows, 640 columns, and 120 bands per pixel. The 120 bands correspond to the visible and infrared range of 471 to 828nm, recorded at a spectral resolution of 3nm.
The images were collected from altitudes in the range of 1200m to 4000m . The spatial resolution of the hyperspectral image (figure left) is approximately 1m for the processed Gvillo field located near the city of Columbia in the central part of Missouri (fig. middle) with associated grid-based locations of ground measurements (fig. right). The display shows combined bands with central wavelengths 471nm, 660nm and 828nm. The images were pre-processed to correct for geometrical distortions, calibrated for sensor noise and illumination, and geo-registered
Figure: A hyperspectral image (left) obtained at 4000m altitude and the Gvillo field located near the city of Columbia in the central part of Missouri (middle) with associated grid-based locations of ground measurements (right). The display shows combined bands with central wavelengths 471nm, 660nm and 828nm.
The training data contained these hyperspectral values and associated ground values of soil electrical conductivity. The field coverage on the date of data collection was bare soil. Among all ground variables, we anticipated to find relationships between hyperspectral values (reflected part of the electro-magnetic (EM) waves in the wavelength range [471nm, 828 nm]) and surface/field characteristics that change electric and magnetic properties according to the EM theory of wave propagation.
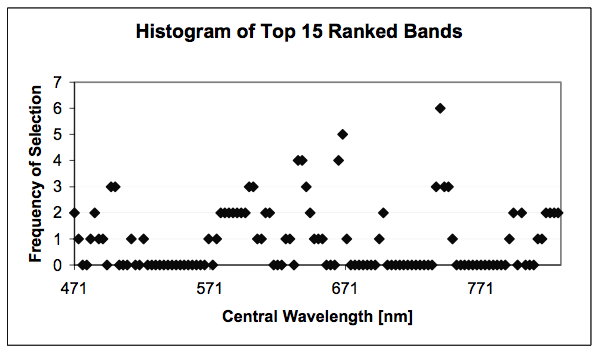
Histogram of top 15 ranked bands by all unsupervised methods.
The results of seven unsupervised band selection methods are shown in Figure above. The processed hyperspectral data came from the training set without using any ground measurements (only 120 hyperspectral band values). The unsupervised methods were implemented in Java and they ran on a Dell PC, Dimension 4100 with a single Intel Pentium III processor and Windows 2000 operating system. The order of unsupervised methods based on their algorithmic computationally efficiency was (1) 1st spectral derivative, (2) 2nd spectral derivative, (3) ratio, (4) contrast, (5) entropy, (6) correlation, and (7) PCAr based methods. The maximum time for processing 190 examples with 120 bands did not exceed 2 seconds.
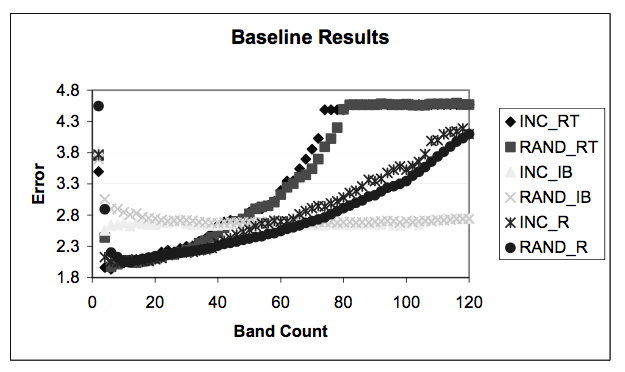
Baseline results obtained for randomly (RAND) and incrementally (INC) selected bands with regression tree (RT), instance based (IB) and regression (R) based supervised methods.
We concluded that the trends for all seven unsupervised methods followed the predicted trends in Figure 2 for supervised regression (Figure 4) and regression tree (Figure 6) based evaluations quite well. Some trend deviation is observed in the regression tree evaluation for band count variable larger that 80 due to the sample size limitation in tree leaves as it was explained in the previous section.
Our recommendation is to select approximately the top 4 to 8 bands with the entropy based unsupervised method followed by a classification model using the regression tree based supervised method. The recommendation is based on computing a weighted average of optimal bands per each supervised method
Summary
In this project we have presented a new methodology for combining unsupervised and supervised methods under classification accuracy and computational requirement constraints that was used for selecting hyperspectral bands and classification methods. We have developed and combined seven unsupervised and three supervised methods to test the proposed methodology. The methodology was applied to the prediction problem between airborne hyperspectral measurements and ground soil electrical conductivity measurements. We conducted a study based on the experimental data that demonstrated the process of obtaining the optimal number of bands, band central wavelengths and the selection of classification methods under classification accuracy and computational requirement constraints. The study concluded that there are about 4-8 most informative bands for the electrical conductivity variable including 7 bands in the red spectrum (600, 603, 636, 639, 642, 666 and 669 nm), 4 bands in the near infrared spectrum (738, 741, 744 and 747 nm) and 2 bands close to the border of blue and green spectra (498 and 501 nm). The proposed band selection methodology is also applicable to other application domains requiring hyperspectral data analysis.
Collaborators
- Peter Bajcsy
Image Spatial Data Analysis Group, NCSA, UIUC - Dennis Andersh
Scientific Applications International Corporation (SAIC), Champaign, IL - Rob Kooper
ISDA, NCSA, UIUC - Peter Groves
Graduate Student, Department of Computer Sciences, UIUC
Papers
- R. Kooper, P. Bajcsy and D. Andersh, "Methodology for Evaluating Statistically Predicted versus Measured Imagery.", Proceedings of the SPIE on Defense and Security 2005 Conference: Algorithms for SAR Imagery XII, 5808-46, March 28-April 1, 2005, Orlando (Kissimmee), Florida USA. [abstract] [pdf 622kB]
- P. Bajcsy and P. Groves, "Methodology For Hyperspectral Band Selection." Photogrammetric Engineering and Remote Sensing 70, p793-802 (2004) [abstract] [pdf 485kB]
- P. Bajcsy, R. Kooper, "Prediction Accuracy of Color Imagery from Hyperspectral Imagery.", Proceedings of the SPIE on Defense and Security 2005, Conference: Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI, 5806-34, March 28-April 1, 2005, Orlando (Kissimmee), Florida, USA. [abstract] [pdf 581kB]